State Space Models

背景与预备知识

连续系统与卷积格式

系统方程：模型由以下线性微分方程定义

$$\dot{x}(t)=Ax(t)+Bu(t),y(t)=Cx(t)$$

$A\in {\mathbb{C}}^{N\times N}$ 为系统矩阵（State Matrix），$B\in {\mathbb{R}}^{C\times 1}$ 为输入矩阵，$C\in {\mathbb{C}}^{1\times N}$ 为输出矩阵。

卷积形式 (Convolution View)：若 $x(0)=0\in {\mathbb{C}}^N$，则上述系统可写为

$$\begin{array}{r}K(t)=C{e}^{At}B,y(t)=(K\ast u)(t)\end{array}$$

其中卷积定义为 $(f\ast g)(t)={\int }_{-\infty }^{\infty }f(\tau )g(t-\tau )d\tau$。

证明：根据常数变异法可解出方程的解

$$x(t)={\int }_0^t{e}^{A(t-\tau )}Bu(\tau )\mathrm{d}\tau \Rightarrow y(t)={\int }_0^{t}C{e}^{A(t-\tau )}Bu(\tau )\mathrm{d}\tau .$$

令 $K(t)=C{e}^{At}B$，则得到

$$y(t)={\int }_0^{t}K(t-\tau )u(\tau )\mathrm{d}\tau \Rightarrow y(t)=(K\ast u)(t).$$

在对角 SSM 的情形下，$A$ 为对角矩阵。此时符号 $A_n,B_n,C_n$ 表示对应参数的元素分量。

Structured State Spaces Model (S4)

HiPPO 矩阵：为了有效地捕捉长期依赖，$A$ 矩阵被初始化为特定的 HiPPO-LegS 矩阵。其元素定义为：

$$A_{nk}=\{\begin{array}{ll}-(2n+1{)}^{1/2}(2k+1{)}^{1/2}& \text{if }n>k\\ -(n+1)& \text{if }n=k\\ 0& \text{if }n<k\end{array}$$

DPLR 结构：为了加速矩阵指数 $e^{At}$ 的计算，S4 将矩阵 $A$ 约束为对角阵加低秩矩阵 (Diagonal Plus Low-Rank, DPLR) 结构：

$$A=A^{(N)}-P{P}^T$$

• 低秩项 $P\in {\mathbb{R}}^{N\times 1}$： 其元素定义为 $P_n=(n+1/2{)}^{1/2}$。
• 正规矩阵 $A^{(N)}\in {\mathbb{R}}^{N\times N}$： 这是一个斜对称矩阵（Skew-symmetric）加上对角阵。其元素满足：

$$A_{nk}^{(N)}=\{\begin{array}{ll}-(n+1/2{)}^{1/2}(k+1/2{)}^{1/2}& \text{if }n>k\\ -1/2& \text{if }n=k\\ (n+1/2{)}^{1/2}(k+1/2{)}^{1/2}& \text{if }n<k\end{array}$$

Diagonal State Spaces (DSS)

核心结论：近期研究（由 Gupta 等人提出）发现，S4 中的低秩项部分（即 $P{P}^T$）在某些情况下可以省略，从而进一步简化模型。DSS 证明了通过对 S4 矩阵进行对角化处理，依然能够保持捕捉长程记忆的能力，同时极大地简化了代码实现和计算流程。

S4D 模型

连续系统的离散：给定步长 $\Delta t$，连续参数 $(A,B)$ 可通过以下两种常用方法转换为离散参数 $(\overline{A},\overline{B})$：

• 双线性变换 (Bilinear):

$$\overline{A}=(I-\Delta t/2A{)}^{-1}(I+\Delta t/2A),\overline{B}=(I-\Delta t/2A{)}^{-1}\cdot \Delta tB$$

• 零阶保持 (ZOH):

$$\overline{A}=\exp (\Delta tA),\overline{B}=(\Delta tA{)}^{-1}(\exp (\Delta tA)-I)\cdot \Delta tB$$

离散卷积核：离散时间 SSM 的输出为 $y=u\ast \overline{K}$，其中离散卷积核 $\overline{K}$ 具有 Krylov 子空间结构：

$$\overline{K}=(C\overline{B},C\overline{A}\overline{B},\dots ,C{\overline{A}}^{L-1}\overline{B})$$

卷积核计算：

A 参数化：为保证稳定性（防止 $t\to \infty$ 时核爆炸），通常强制 $A$ 的实部为负。$A=-\exp (A_{Re})+i\cdot A_{Im}$ （或使用 ReLU 等激活函数）。

对角状态矩阵的初始化

对角系数矩阵的稠密性

命题：任意状态空间模型 $(A,B,C)$ 等价于 $(V^{-1}AV,V^{-1}B,CV)$ 模型，其中 $V\in {\mathbb{C}}^{N\times N}$ 为可逆矩阵。

证明：考虑如下线性系统

$$\dot{x}(t)=Ax(t)+Bu(t),y(t)=Cx(t).$$

令 $x=V\ell (t)$，则上述系统等价于 $V\dot{\ell }(t)=AV\ell (t)+Bu(t)$ 以及 $y(t)=CV\ell (t)$，因此我们得到新系统

$$\dot{\ell }(t)=V^{-1}AV\ell (t)+V^{-1}Bu(t),y(t)=CV\ell (t).$$

命题：所有 ${\mathbb{C}}^{N\times N}$ 中的可对角化矩阵集合 $\mathcal{D}\subset {\mathbb{C}}^{N\times N}$ 在 ${\mathbb{C}}^{N\times N}$ 中稠密。

• 不可对角化矩阵之所以“稀有”，是因为它要求特征方程 $\det (\lambda I-A)=0$ 必须有重根，并且这些重根对应的几何重数小于代数重数。
• 上述命题证明了纯对角矩阵在数学上可以表示任何线性系统，但这并不意味着能通过梯度下降轻易地“练”出这个效果。事实上 Albert Gu 等人证明了如果使用随机初始化，稠密实矩阵和对角复矩阵的表达能力都较差。
• 数值稳定性至关重要。具有相同频谱（即等价于相同对角阵）的两个初始化可能有截然不同的性能表现。

S4D 格式推导

S4D-LegS：令 $A=A^{(N)}-P{P}^{\top }$ 为 HiPPO-LegS 矩阵。当状态维度 $N\to \infty$ 时，由正规部分 $A^{(N)}$ (即 S4D-LegS) 生成的 kernel bases $K_{A^{(N)},B/2}(t)$ 收敛于原始 S4 的 kernel bases $K_{A,B}(t)$。

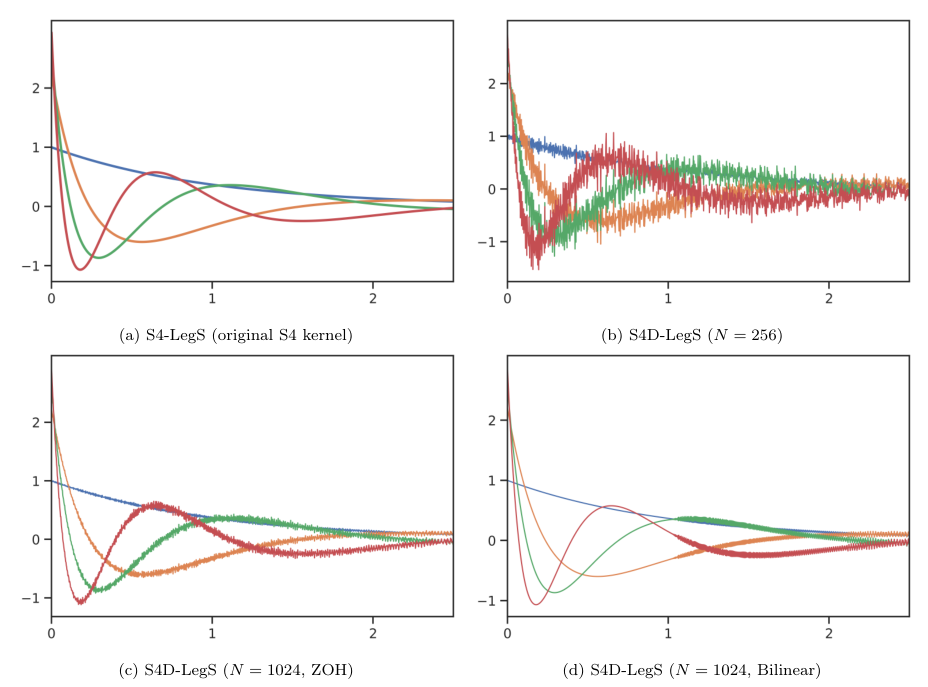
S4D-Inv：为了进一步简化 S4D-LegS，我们分析 $A^{(D)}$ 的结构。实部恒定为 $\mathrm{Re}(A)=-\frac{1}{2}$，虚部遵循逆缩放律。猜测当 $N\to \infty$ 时，虚部 $\mathrm{Im}(A{)}_n\approx \Theta (n^{-1})$。

$$A_n=-\frac{1}{2}+i\frac{N}{\pi }\left(\frac{N}{2n+1}-1\right)$$

S4D-Lin：更简单的初始化 S4D-Lin 近似于傅里叶级数频率（对应 S4-FouT 变体）。其基函数 $e^{tA}B$ 表现为阻尼傅里叶基函数。

$$A_n=-\frac{1}{2}+i\pi n.$$