参考文献:Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network
理论起源:微分方程视角
微分方程视角:RNN 的动力学方程可由一阶非齐次 ODE 推导而来。设 为 维状态信号向量,其随时间 的演化可表示为:
- 是 维输入信号向量, 为 为状态向量;
- 是 维向量函数,通常依赖于 和 ,即 ;
- 是常数 维向量(偏差项)。
加性模型:这里采用加性模型 (Additive Model),将 分解为三个独立项的线性组合:
记 分别表示状态、读出和输入的延迟时间常数。
- 状态反馈项 :表示状态信号自身的延迟影响("模拟"分量)
- 读出反馈项 :表示经过非线性变换后的读出信号的延迟影响:
- 外部输入项 :表示外部输入信号的延迟影响
延迟微分方程 (DDE) 系统:
线性系数 DDE:当上述函数为线性时,可以转化为具有线性矩阵系数的非线性 DDE:
其中 分别为对应项的系数矩阵。
简化模型 (The Simplified Model):通过以下特定约束,可将通用模型简化为包含 Continuous Hopfield Network 和 Cellular Neural Network 的特例形式:
- 单项约束:设 (每种反馈仅有一项)。
- 延迟约束:设 (状态和输入无延迟),仅保留读出信号的单一延迟 。
- 矩阵重命名:。
时间离散与 RNN 公式
命题(离散化公式):使用向后欧拉离散上述方程可得到
证明:设采样时间步长为 ,时间 。使用后向欧拉法近似导数:
令延迟时间 等于单步采样时间 (即 ):
这里采用了简化记号 。注意方程右侧使用了 时刻的 和 (后向法的特性),但使用了 时刻的 (由延迟 决定)。接着
定义 ,并在方程两边左乘 ,得到:
将索引向前平移一步 () 可得结论。
标准 RNN 形式:为了进一步简化表示,定义新的权重矩阵和偏差向量:
其中
- : 状态自身的递归权重(State-to-State)。
- : 读出信号(即上一时刻的激活值)的反馈权重(Readout-to-State)。
- : 当前输入的权重(Input-to-State)。
稳定性分析
稳定性条件:上述系统稳定的条件是矩阵 的所有特征值必须位于复平面的单位圆内。
标准 RNN 定义:在实际应用中,常作进一步简化以获得最简形式:
- 单位时间步长:设 。
- 快速状态衰减:假设矩阵 为对角阵且对角元为很大的负数(),这意味着状态的衰减非常快。
- 忽略状态记忆:由此导致 为对角阵且元素为很小的正数。在这种情况下,状态信号 对当前轨迹的显式影响(第一项)可以忽略不计(尽管通过 的隐式影响依然存在)。
- 忽略 项(即设 )
我们得到最常见的标准 RNN 定义,其中 通常是 函数
在此简化下,系统的稳定性完全取决于 的特征值 。在“小信号”区域(),稳定性的充要条件是 。
Diagonal SSM 系统
连续 Diagonal SSM 系统:一般考虑如下 Diagonal SSM LTI 系统
其中 ,, (一般使用取实部操作),,,。
ZOH 离散化公式:连续矩阵转化为离散矩阵:
其中 是可学习的参数, 不参与离散。
离散递归方程 (RNN Mode):
能控性与能观性分析
Kalman 结论保证如果连续系统是能控/能观的,那么离散化系统也是能控的,除非采样周期 满足特定的病态条件(未调研)。下面默认使用连续系统矩阵。
能控性分析
能控性矩阵:能控性矩阵为:
能控性分析:Diagonal SSM 能控当且仅当 的特征值互不相同且 所有元素非零。
证明:设 ,且 。计算能控性矩阵 的各项:
- 第 1 列 ():
- 第 2 列 ():
- 第 列 ():
此时,能控性矩阵 可以分解为两个矩阵的乘积:
即 。为了使 满秩 (),必须满足两个条件:
- 输入必须能直接影响每一个状态分量:,即 。
- 范德蒙德矩阵满秩:,而 。这要求 的所有特征值 必须互不相同 (Distinct Eigenvalues)。
能观性分析
能观性矩阵:
能观性分析:Diagonal SSM 能观当且仅当 所有特征值不相同, 所有元素非零。
证明:与能控性类似。
背景与预备知识
连续系统与卷积格式
系统方程:模型由以下线性微分方程定义
为系统矩阵(State Matrix), 为输入矩阵, 为输出矩阵。
卷积形式 (Convolution View):若 ,则上述系统可写为
其中卷积定义为 。
证明:根据常数变异法可解出方程的解
令 ,则得到
在对角 SSM 的情形下, 为对角矩阵。此时符号 表示对应参数的元素分量。
Structured State Spaces Model (S4)
HiPPO 矩阵:为了有效地捕捉长期依赖, 矩阵被初始化为特定的 HiPPO-LegS 矩阵。其元素定义为:
DPLR 结构:为了加速矩阵指数 的计算,S4 将矩阵 约束为对角阵加低秩矩阵 (Diagonal Plus Low-Rank, DPLR) 结构:
- 低秩项 : 其元素定义为 。
- 正规矩阵 : 这是一个斜对称矩阵(Skew-symmetric)加上对角阵。其元素满足:
Diagonal State Spaces (DSS)
核心结论:近期研究(由 Gupta 等人提出)发现,S4 中的低秩项部分(即 )在某些情况下可以省略,从而进一步简化模型。DSS 证明了通过对 S4 矩阵进行对角化处理,依然能够保持捕捉长程记忆的能力,同时极大地简化了代码实现和计算流程。
| 符号 | 全称 | 说明 |
|---|---|---|
| HiPPO-LegS | 原始的 HiPPO 矩阵(下三角矩阵),在 S4 中使用 | |
| HiPPO-LegS-N | 矩阵 的正规部分(Normal part),具有斜对称性。 | |
| HiPPO-LegS-D | 矩阵 的对角化形式,即其特征值组成的对角阵。在 DSS 中使用。 |
S4D 模型
连续系统的离散:给定步长 ,连续参数 可通过以下两种常用方法转换为离散参数 :
- 双线性变换 (Bilinear):
- 零阶保持 (ZOH):
离散卷积核:离散时间 SSM 的输出为 ,其中离散卷积核 具有 Krylov 子空间结构:
卷积核计算:
A 参数化:为保证稳定性(防止 时核爆炸),通常强制 的实部为负。 (或使用 ReLU 等激活函数)。
| 方法 | 结构 (Structure) | 核计算 (Kernel Comp.) | 离散化 (Discretization) | 约束 | 可训练 | 初始化 |
|---|---|---|---|---|---|---|
| S4 | DPLR | Cauchy | Bilinear | Yes | HiPPO | |
| DSS | Diagonal | Softmax | ZOH | None (id) | No | HiPPO-D |
| S4D | Diagonal | Vandermonde | Any (Bilinear/ZOH) | / ReLU | Optional | Various |
对角状态矩阵的初始化
对角系数矩阵的稠密性
命题:任意状态空间模型 等价于 模型,其中 为可逆矩阵。
证明:考虑如下线性系统
令 ,则上述系统等价于 以及 ,因此我们得到新系统
命题:所有 中的可对角化矩阵集合 在 中稠密。
- 不可对角化矩阵之所以“稀有”,是因为它要求特征方程 必须有重根,并且这些重根对应的几何重数小于代数重数。
- 上述命题证明了纯对角矩阵在数学上可以表示任何线性系统,但这并不意味着能通过梯度下降轻易地“练”出这个效果。事实上 Albert Gu 等人证明了如果使用随机初始化,稠密实矩阵和对角复矩阵的表达能力都较差。
- 数值稳定性至关重要。具有相同频谱(即等价于相同对角阵)的两个初始化可能有截然不同的性能表现。
S4D 格式推导
S4D-LegS:令 为 HiPPO-LegS 矩阵。当状态维度 时,由正规部分 (即 S4D-LegS) 生成的 kernel bases 收敛于原始 S4 的 kernel bases 。
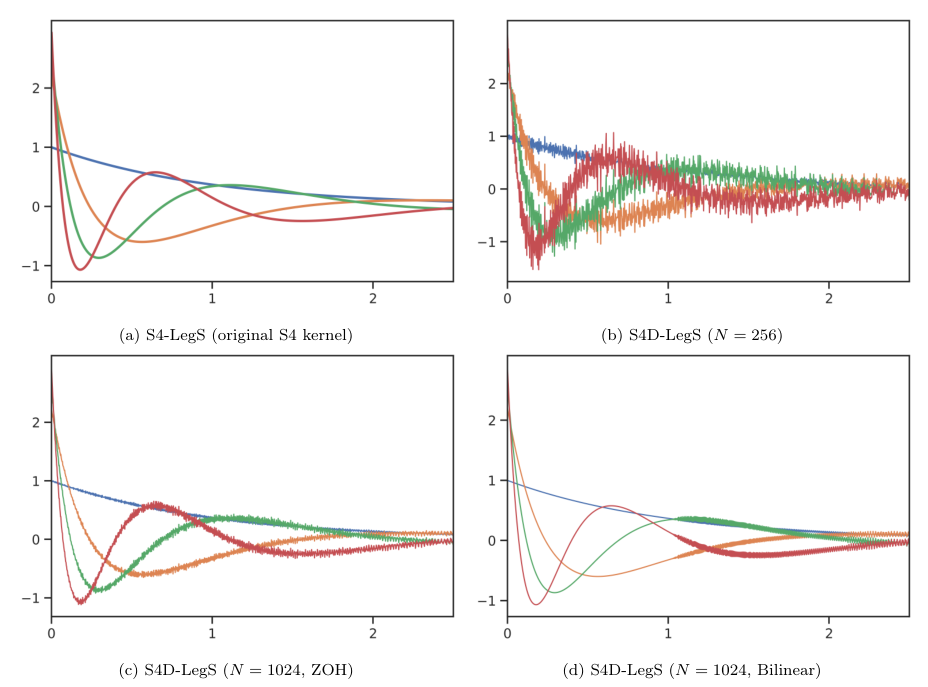
S4D-Inv:为了进一步简化 S4D-LegS,我们分析 的结构。实部恒定为 ,虚部遵循逆缩放律。猜测当 时,虚部 。
S4D-Lin:更简单的初始化 S4D-Lin 近似于傅里叶级数频率(对应 S4-FouT 变体)。其基函数 表现为阻尼傅里叶基函数。
| 方法 | 实部 | 虚部 分布 | 数学解释 |
|---|---|---|---|
| S4D-LegS | 复杂 (来自 HiPPO 对角化) | 渐近等价于 S4-LegS | |
| S4D-Inv | (逆律) | S4D-LegS 的闭式近似 | |
| S4D-Lin | (线性) | 阻尼傅里叶级数 (S4-FouT) |
卷积核格式推导
递推格式展开:考虑如下离散后的 S4D 系统,其中 ,
其中 ,,,,,。我们有
卷积核定义:卷积核可以定义为如下
由于 是对角矩阵, 是向量, 是向量,因此 是一个数,可以写为
从而
其中 满足如上式子。
Pytorch 实现:先根据 A, B, C, L 计算出 Kernel K (L,)。然后再转换到频域计算。
import torch
import torch.fft
def compute_ssm_kernel(A, B, C, L):
"""
步骤 1: 生成卷积核 K
对应公式: K_t = sum_{n=1}^N C_n * (A_n)^t * B_n
参数:
A: (N,) 复数对角矩阵的对角元素
B: (N,) 复数输入投影
C: (N,) 复数输出投影
L: 序列长度
返回:
K: (L,) 复数卷积核
"""
# 1. 构造时间步向量 t = [0, 1, ..., L-1]
# shape: (L)
t = torch.arange(L, device=A.device)
# 2. 计算 A 的幂次 (A_n)^t
# 利用广播机制: (N, 1) ** (L) -> (N, L)
# 这一步计算了所有状态 n 在所有时刻 t 的衰减项
A_powers = torch.pow(A.unsqueeze(-1), t)
# 3. 计算各项乘积 C_n * (A_n)^t * B_n
# term shape: (N, L)
term = (C * B).unsqueeze(-1) * A_powers
# 4. 对状态维度 N 求和 (sum_{n=1}^N)
# 这一步将 N 个独立状态的响应混合成一个系统的脉冲响应
K = torch.sum(term, dim=0)
return K # shape: (L,)
def fft_convolution(x, K):
"""
步骤 2: FFT 卷积加速
对应公式: y = x * K
参数:
x: (Batch, L) 实数输入序列
K: (L,) 复数卷积核
返回:
y: (Batch, L) 实数输出序列
"""
L = x.shape[-1]
# 1. 确定 FFT 长度 (通常设为 2*L 以避免循环卷积混叠)
fft_len = 2 * L
# 2. 输入 x (实数) -> 频域
# 使用 rfft 因为 x 是实数,只计算一半频谱
x_f = torch.fft.rfft(x, n=fft_len)
# 3. 卷积核 K (复数) -> 频域
# 使用 fft 因为 K 本身是复数
k_f = torch.fft.fft(K, n=fft_len)
# 4. 对齐频谱
# rfft 得到的频谱长度为 fft_len//2 + 1
# 我们需要截取 k_f 对应的前半部分正频率
k_f = k_f[..., :x_f.shape[-1]]
# 5. 频域乘法 (对应时域卷积)
y_f = x_f * k_f
# 6. 逆变换回时域 + 截断
y = torch.fft.irfft(y_f, n=fft_len)
y = y[..., :L] # 去掉补零产生的部分
return y
- 原论文:Arxiv
- 2025.12.10 完成笔记
- 2025.12.11 补充 SSM 经典模型的能观性和能控性,具体见 Diagonal SSM
预备知识
离散线性时不变系统 (Discrete LTI Systems)
定义(离散 LTI 系统):设 为一个离散线性时不变 (Linear Time-Invariant, LTI) 系统,其状态方程描述如下:
- 为状态向量 (state);
- 为输入向量 (input);
- 为输出向量 (output);
- 系统矩阵维度为 。
假设(稳定性 Stability):系统是稳定的,即矩阵 的所有特征值模长均小于 1:
假设(可控性 Controllability):系统对 是可控的。即存在有限时间,使得状态 可以从任意初始状态被控制(驱动)到任意最终状态。可控性矩阵 必须满秩:
如果系统不能控,则状态空间中存在某些维度(子空间),无论输入 是什么,都无法影响这些维度的状态。
假设(可观性 Observability):系统对 是可观的。即通过观测有限时间内的输出 和输入 ,足以确定初始状态 。能观性矩阵 必须满秩:
如果系统不可观,意味着状态空间中存在某些维度的变化,根本不会反映在输出 中。
离散 Lyapunov 方程理论 (Discrete Lyapunov Equation)
Lyapunov 方程起源:设系统的输入 不是确定的控制量,而是零均值的高斯白噪声 ,其协方差为 (即 )。
我们想知道当时间趋于无穷时,系统状态 的分布是什么样的?定义状态的协方差矩阵为 。我们可以推导 随时间的变化:
由于 是过去的状态,与当前的噪声 不相关(独立),中间两项期望为 0。于是得到:
如果系统是稳定的( 使得能量衰减),且噪声源源不断地输入(),那么最终状态的“云团”大小(协方差)会达到一个动态平衡。此时 。
定义(离散 Lyapunov 方程):给定矩阵 和对称矩阵 ,寻找对称矩阵 满足:
或者写作等价形式 。
Lyapunov 方程有两种理解:
- 输入噪声:方程解描述了给定持续不断的随机误差扰动 ,系统最终会在多大的范围(方差)内波动。
- 输入控制:方程解描述了给定输入控制 ,对系统造成的能量大小/状态变化。
推导(级数解的构造):我们可以通过迭代法直观地构造解。假设 满足 ,我们将 自身反复代入方程右边:
当 时,如果余项 ,则我们得到级数解:
定理(存在性与唯一性):若矩阵 是稳定的(即谱半径 ),则对于任意对称矩阵 :
- 级数 绝对收敛,且该级数是离散 Lyapunov 方程的唯一解。
- 若 是正定 (或半正定) 的,则解 也是正定 (或半正定) 的。
这个方程本质上是在计算一个线性系统在无限时间内的“能量累积”。只有当系统是稳定的(能量会耗散,而不是无限增长),这个累积和(级数)才是一个有限值。
可控性与可观性格拉姆矩阵 (Gramians)
Gramians 提供了比秩判据更丰富的信息:它们不仅告诉我们状态是否可控/可观,还量化了控制或观测的难易程度(能量代价)。
定义(离散可控性格拉姆矩阵):假设上述系统是稳定且可控的,则存在唯一的对称正定矩阵 满足离散 Lyapunov 方程:
物理意义:我们要寻找一个能量最小的输入序列 ,把系统从零状态 驱动到目标状态 。根据系统方程 ,经过 步后,最终状态 可以写成输入的线性组合:
即 。我们需要最小化输入能量 ,同时满足约束 。这是一个标准的最小范数解问题(求伪逆)。根据拉格朗日乘子法,最优解 为:
现在,我们计算这个最优输入的能量 :
当 时,矩阵 正是我们的 可控性 Gramian 。所以:
物理意义: 衡量了到达某个状态所需的最小输入能量,准确来说是 ,因此 的特征值越大,所需的能量越小。
定义(离散可观性格拉姆矩阵):假设上述系统是稳定且可观的,则存在唯一的对称正定矩阵 满足离散 Lyapunov 方程:
其显式解形式为:
物理意义: 衡量了 能产生多少输出能量,。
平衡实现 (Balanced Realizations)
定义(状态空间实现):离散时间线性系统 由其输入-输出映射完全刻画:
若四元组 及状态 能够实现上述映射,则称其为 的一个实现 (Realization)。
注:实现不唯一。若 是一个实现,则对于任意可逆矩阵 , 也是同一个系统的实现。
定义(最小实现 Mimimal):若一个实现既是可控的又是可观的,则称其为最小实现。其状态维度 称为实现的阶数 (Order)。
定义(平衡实现 Balanced):若一个实现的格拉姆矩阵满足 ,则称该实现是平衡的。此时记公共矩阵为 ,称为平衡系统的格拉姆矩阵。
Balanced realization 的意义是给系统找一把“公平的尺子”,让所有状态在“输入端”和“输出端”的重要性被同等看待。即对于某个状态 ,对于输入端 和输出端 是同等重要的。
定理(Antoulas, 2005):任意稳定、最小的离散 LTI 系统都存在一个平衡实现,其可控性和可观性格拉姆矩阵相等且为对角阵:
其中 称为 Hankel 奇异值 (Hankel Singular Values, HSV)。
计算方法:HSV 也可以通过非平衡实现的格拉姆矩阵计算得出:
Hankel 奇异值量化了每个状态的联合可控性和可观性。大的 对应既容易被控制又容易被观测的状态(即对系统动力学贡献大的状态)。
SRBT 算法:找到变换矩阵 同时对角化 和 。核心思想为利用 和 的“平方根”(Cholesky 因子)以及 SVD 分解来构造 。
- Cholesky 分解 (求平方根):由于 是对称正定矩阵,对其进行 Cholesky 分解:
其中 为下三角矩阵。
- 奇异值分解 (SVD):计算交叉乘积矩阵 并进行 SVD 分解
其中 即为包含 Hankel 奇异值的对角阵, 为正交矩阵。
- 构造变换矩阵:平衡变换矩阵 及其逆矩阵 可由下式给出:
直观理解: 融合了可控性信息 () 和可观性信息 (),将系统投影到一个两者“势均力敌”的坐标系中。
平衡截断 (Balanced Truncation)
平衡截断是一种模型降阶 (Model Order Reduction, MOR) 方法,利用 Hankel 奇异值的大小对状态进行取舍。
定义(平衡截断步骤):考虑一个稳定、最小的平衡实现 ,其格拉姆矩阵 ,其中 包含较大的 个奇异值, 包含剩余的 个较小奇异值。将系统矩阵分块:
其中 。
性质(降阶系统):由 定义的降阶系统 是稳定的,且满足以下误差界:
这表明截断误差由被丢弃的 Hankel 奇异值之和控制。
Hermitian 矩阵的谱稳定性 (Spectral Stability)
在训练状态空间模型 (SSMs) 时,梯度下降会逐步修改状态矩阵。了解这种扰动如何影响 Hankel 奇异值至关重要。
定理(Weyl, 1912):设 和 为 阶 Hermitian 矩阵(实对称矩阵),令 。设 表示 的第 大特征值。则 在 Hermitian 矩阵空间上关于算子范数是 Lipschitz 连续的:
物理意义: 的每个特征值的波动幅度不会超过扰动矩阵 的最大绝对特征值。这为训练过程中的谱变化提供了理论上界
CompreSSM 算法
CompreSSM 算法的核心思想是在训练过程中动态地对 SSM 层的线性系统进行平衡截断。该算法针对每一个 SSM 块(Block)独立进行。
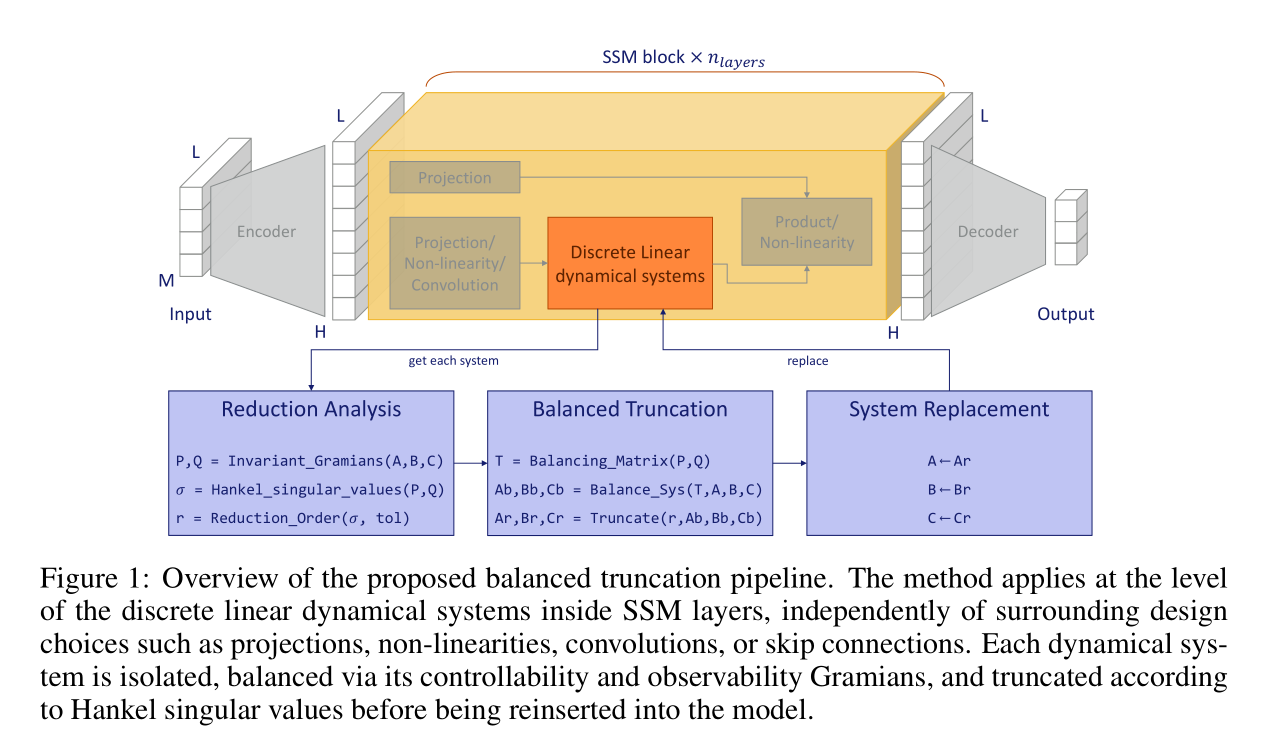
算法输入:模型权重中的离散线性系统矩阵 。当前系统阶数(秩)。能量阈值 (预设超参数)。
Reduction Analysis 部分:求出系统中哪些状态是重要的
- 提取矩阵:从模型权重中提取 。
- 求解 Gramians:解离散 Lyapunov 方程获得 和 。 显示出哪些状态容易被输入激发(存能量), 显示出哪些状态容易影响输出(放能量)。当 是对角矩阵时, 的无穷级数可以用等比数列求和计算。
- 计算 HSV:计算 Hankel 奇异值 。 是第 个状态的【综合重要性得分】。
- 确定截断阶数 :找到满足总能量比例 的最小阶数 :
Balanced Truncation 部分:
- 判断是否截断:若 (即存在冗余),计算平衡变换矩阵 。否则,保持系统不变。
- 执行平衡变换:将系统转换到对角平衡实现:
- 执行截断:保留前 个维度(使用张量切片表示):
System Replacement 部分:将模型中的原始矩阵替换为截断后的矩阵:
训练中的动态降阶 (In-Training Reduction)
CompreSSM 主张在训练的早期(如学习率预热阶段)进行降阶。这依赖于以下理论和实验观察,证明了训练动力学有利于早期截断。
Hankel 奇异值的连续性
在梯度下降过程中,模型参数 发生微小变化 ,导致系统变为新的动力系统 。我们需要保证这种微小变化不会导致 Hankel 奇异值(即状态的重要性)发生剧烈跳变。
定义:令 ,其特征值即为 Hankel 奇异值。 对于系统扰动是连续的,记 。
引理 (训练更新下 HSV 的连续性): 根据 Weyl 定理,在梯度步之间,每个 Hankel 奇异值的变化幅度有上界:
这意味着状态的重要性评分 是关于模型权重的连续函数,不会突变。
相对次序的稳定性 (Stability of Relative Ordering)
仅有连续性是不够的。如果 HSV 的相对大小频繁交叉(即一个不重要的状态突然变得非常重要),那么早期的截断就是危险的。
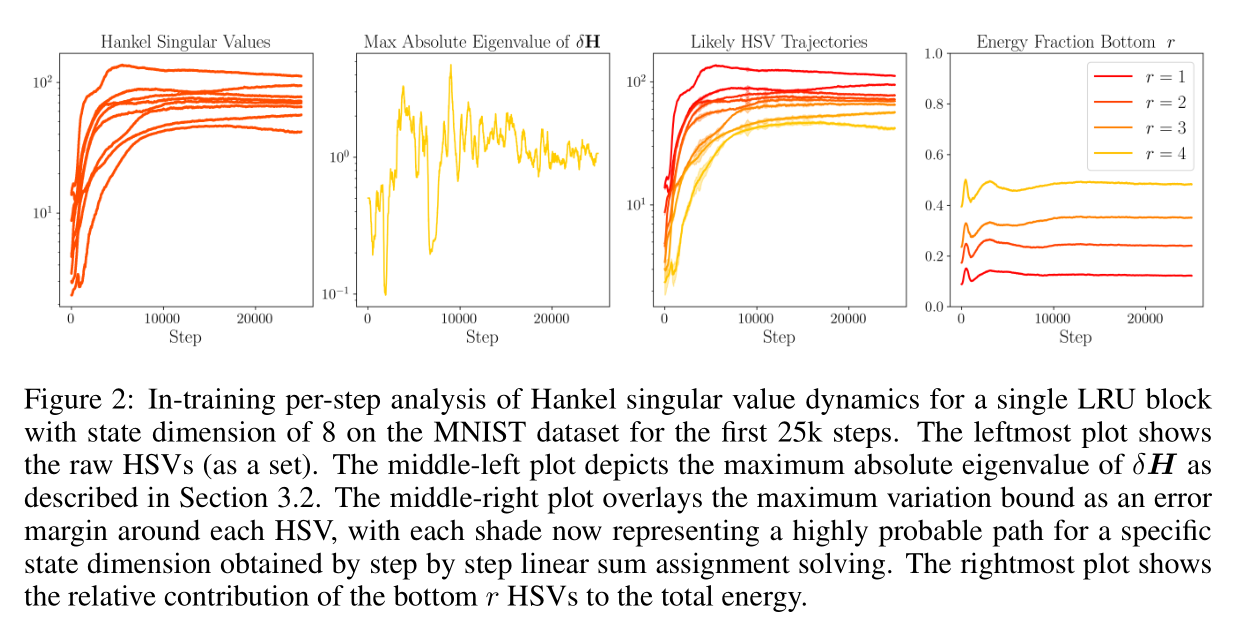
实验观察:
- 图1 次序保持:实验表明 Hankel 奇异值的相对次序在训练初期迅速稳定。大奇异值保持较大,小奇异值保持较小。
- 图2 连续性:每步的 最大为 的量级,与 Singular Value 本身 的量级比起来可以算是连续的。
- 图3 次序保持:对每个维度进行追踪,次序保持稳定。
- 图4 能量贡献:底部 个(被截断的)维度的累积能量贡献在训练过程中始终维持在低位,很少获得实质性的能量增长。
结论: 在训练早期被识别为“可忽略”的维度,通常在整个训练过程中都保持可忽略状态。因此,早期截断决策与最终的重要性排名很少冲突,这使得 In-Training Reduction 既有效又鲁棒。
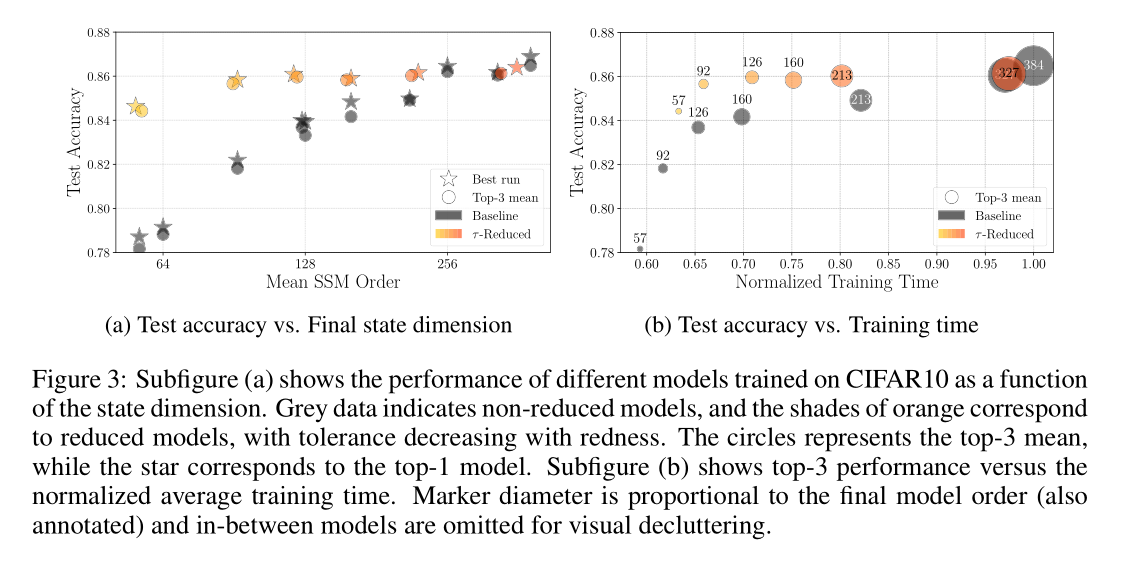
实验结果
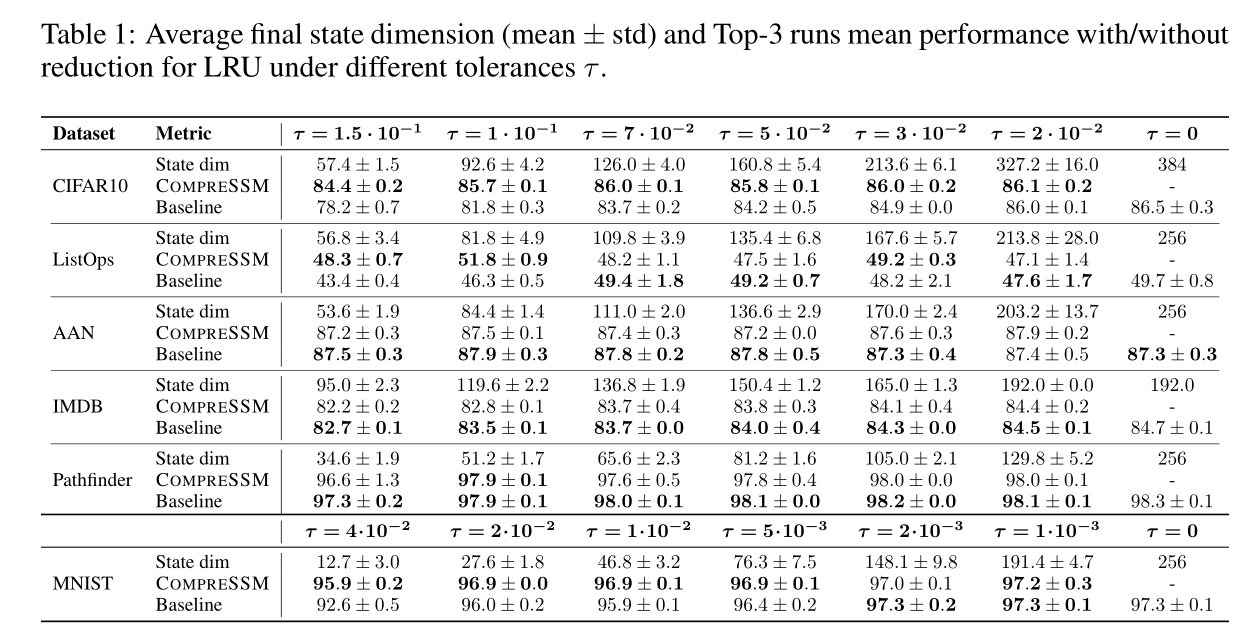
- CompreSSM 模型:从大模型开始(如 CIFAR10 初始维度 384),训练中途自动变小。
- Baseline 模型:直接从一开始就训练小模型。